[最も好ましい] 空間ベクトル 大きさ 公式 937786-空間ベクトル 大きさ 公式

2次元ベクトル (x,y)の大きさ = √ x² y² そして、上記の計算で得られた2次元ベクトルの大きさとzを使って最終的なベクトルの大きさを求めます。 例 3次元ベクトル (1,80,30)の大きさ (長さ)を求める 最初にxとyの2次元ベクトルの大きさを求める。要するに、ベクトルは数を表す文字と同じように計算してもよいということである。 5 ベクトルの大きさ n 次元ベクトルV の大きさをjVj またはjjVjj と表し、以下の公式で定義する。 jVj = v u u t i=1 Vi 2 三次元空間の場合は、jVj = q Vx 2 V y 2 V z 2 となる。ベクトルの大きさは、ノルムまたは長空間ベクトルの成分の解答 → b = √ 2 2 3 2 ( − 4) 2 = √ 29 『成分表示された空間ベクトルの大きさ』 2 → a − → b 3 → c = 2 ( 1 1 1 ) − ( 2 3 − 4) 3 ( − 2 5 4) = ( 2 − 2 − 6 2 − 3 15 2 4 12) = ( − 6 14 18) → a → b → c を成分で表すと → a → b → c = ( 1 9 1) となるので → a → b → c = √ 1 2 9 2 1 2 = √ 『成分表示された空間ベクトルの大きさ』

高校数学b ベクトル A Tb の大きさの最小値と図形的意味 受験の月

空間ベクトル 大きさ 公式

空間ベクトル 大きさ 公式- このページでは、数学Bの「平面ベクトル」の公式をまとめました。 空間ベクトルの公式は「空間ベクトル 公式一覧」で説明しているので、チェックしてみてください。 問題集を解く際の参考にしてください！ ベクトルのなす角の公式 \( \large{ \color{red}{ \displaystyle \cos \theta = \frac{ \vec{ a } \cdot \vec{ b } }{ \left \vec{ a } \right \vec{ b } } } } \) \( \color{red}{ \displaystyle = \frac{ a_1 b_1 a_2 b_2 a_3 b_3 }{ \sqrt{ {a_1}^2 {a_2}^2

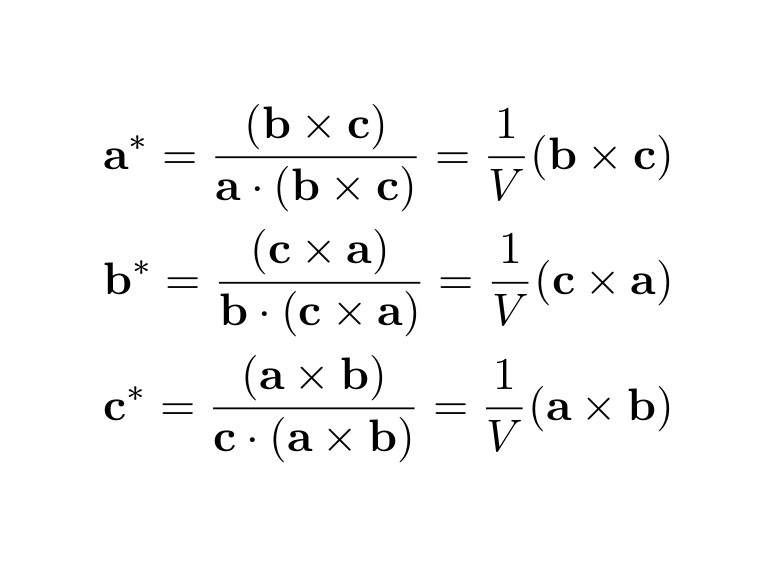
逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction

2 第1 章 ベクトル空間 (2) スカラー倍 K の要素r とV の要素x の対(r;x) に対してV の要素rx を対応させる演算 が定義されていて, 任意のx;y;z 2 V, r;s 2 K に対して次の(i)～(viii) が成り立つときV をK 上のベクトル 空間という またV の要素をベクトルと呼び, それに対しK の要素をスカラーと呼ぶ平面が空間になろうが考え方は一緒です。 ちなみに、原点Oから点Aの距離の求め方は次の公式を用います。 ・ 長方形の辺を、ベクトルを使って表してみましょう ・ 空間図形の基本～体を空間に慣らしましょう～ ・ 同じ平面上にある点について考えてみUの逆ベクトルと呼ばれ、−uと書かれる。 (vii) ベクトルu,v ∈ V のベクトル差は、u−v = u(−v)と定義される。特に、任意のベ クトルu∈ V に対して、u−u= 0である。 補題4 ベクトル空間(V,, )をおいておく。 (1) 零ベクトルについては、ただ一つが存在する。 2

空間のベクトルでは、平面の時と比べてパラメータが1つ増えますが、平面上のベクトルの公式等がそのまま使えます。 空間のベクトルでの公式 空間のベクトルでも同じように成立する公式を紹介していきます。まず、2点\(A(x_1 , y_1 , z_1) , B(x_2 , y_2 , z_2)\) 間1．． 曲線のベクトル方程式 1 3次元ユークリッド空間の位置を示す位置ベクトルr をパラメーター t を用いて r ＝ r (t)＝(x(t),y(t),z(t)) ； a≦t≦b と表わすとき，このベクトルの(先端の)軌跡は3次元空間の曲線を表します 。 これを曲線のベクトル方程式といいます。ル空間、K = C のときn 次元複素数ベクトル空間と呼ぶ。(次元の定義) 13) 例2 Mmn(K) = K を成分にもつ(m,n) 行列全体 は行列の和とスカラー積に関してK 上のベクトル空間となる。これらはベクトル空間と してはKmn と同型(ベクトル空間の同型) 31) であるが、(l,m

ベクトルの内積 (inner product, dot product, scalar product) と外積 (outer product, cross product, vector product) という演算を用いると幾何の問題を解く考え方が簡単になります。 幾何学における内積や外積はもともと3次元空間上で定義されるものなので，まずは3次元空間上で正射影ベクトルの公式の証明 正射影ベクトルの公式は，ベクトル a undefined \overrightarrow{a} a とベクトル b undefined \overrightarrow{b} b が与えられたときに射影したベクトル v undefined \overrightarrow{v} v を求める公式です。 正射影ベクトルの公式の証明は難しくありません。62 ベクトル公式 ついでにベクトル演算子に関連する公式を掲げておこう．以下の公式はどの座標系でも 成立する重要なベクトル公式である．ここでは直角座標系における確認を示しておく． ( A) 0 ( A)= x A x y A y z A z = x A z y – A y z y A x z – A z x z Ay x –

ベクトルの外積とは 公式 性質 例 証明付 理数アラカルト

高校数学b ベクトル A Tb の大きさの最小値と図形的意味 受験の月

公式から外積を求められる理由① なぜこの方法でベクトルの外積を求めることができるのでしょうか？ 実は、これは以下のように基底ベクトル \(\hat{\imath}\)、\(\hat{\jmath}\) 、\(\hat{k}\) を1列目の要素に、ベクトル \(\vec{v}\)、\(\vec{w}\) をそれぞれ2列目と3列目の要素にした3次行列式を解くというベクトル方程式とは空間上の点がある規則(直線上，平面上，円上，球上にあるetc)をベクトルで表現しようと言う主旨のものです． と思います．型1のような与えられ方をしていてもその2ベクトルの外積から 法線ベクトルを求めればすぐに公式どおりのMathAquarium例題空間のベクトル 3 3 空間のベクトルの成分表示 (1) a ＝(－3，1，－2)， b ＝ (1，0，2)のとき，－ ＋ 2b を成分で表せ。また，その大きさを求めよ。 (2) ＝(－3，1，－2)， ＝(1，0，2)， c ＝ (3，－3，1)のとき， p ＝ (1，2，3)を p ＝ sa ＋ tb ＋ uc の 形で表せ。

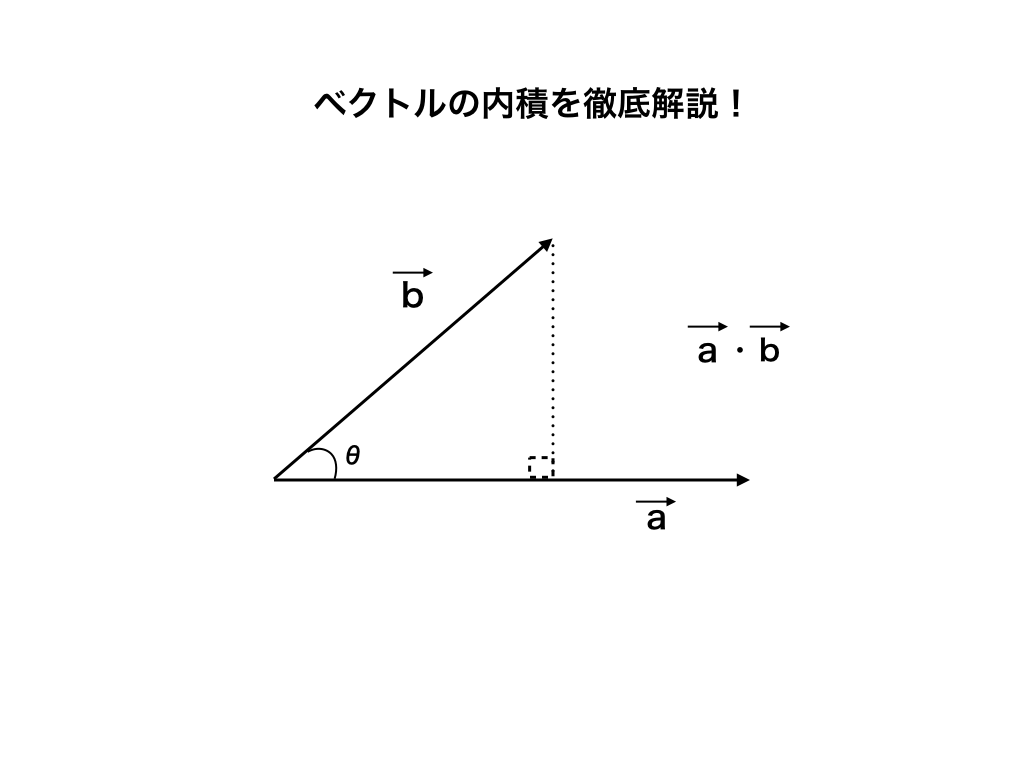
内積とは 定義と求め方 公式を解説 ベクトルの掛け算を分かりやすく

ベクトル 高校物理の備忘録

問題 上の公式を確かめよ 空間曲線 3 次元空間での滑らかな曲線を考えよう．ある点の位置ベクトルを出発点から測っ た曲線の長さsの関数として考える；r(s)．単位接線ベクトルは ˆt = dr ds (226) ここで lim ∆s→0 ∆r ∆s = 1 (227)大きさが5のベクトルを5で割ると大きさ1のベクトルになります(向きは変わりません)。 一般に，ベクトル をその大きさで割ったもの は，と同じ向きで大きさ1のベクトルになります。 大きさ1のベクトルを単位ベクトルといいます。(1)クーロンの法則とは 二つの点電荷があると、お互いに力を及ぼし合います。 この力のことを静電力（クーロン力）とよび、次のような性質があります。 「二つの点電荷間に働く静電力 〔n〕（ニュートン）の大きさは、両電荷 の積に比例し、電荷間の距離 の2乗に反比例する。

48s96ub7b0z5f Net Kuukan Bekutoru Gaiseki

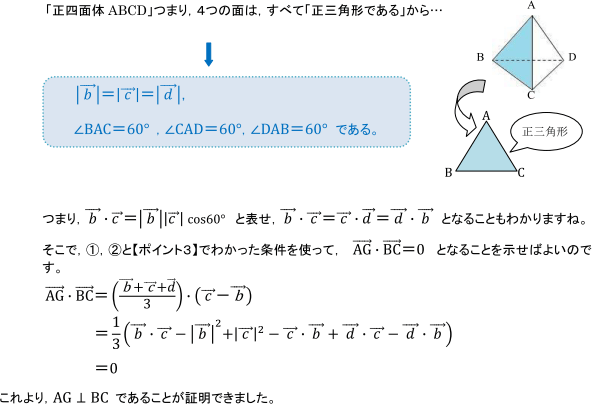
空間ベクトル 垂直であることの証明の仕方 数学b 定期テスト対策サイト

の ベクトルの大きさ は， ∣∣→ a ∣∣ =√ax2ay2 a → = a x 2 a y 2 で計算できる（ 2点間の距離 を参照）． 成分表示 で表された 座標空間 におけるベクトル 平面における曲線のベクトル表示を説明したが、正直 今までの 「\(y=\bigcirc\bigcirc\)」でよくね？ って思った人も多いはずである。 実は、この曲線をベクトル表示する恩恵は 空間における曲線 に対しては、如実に感じられる。 例として、次の らせん曲線 を式で表現してみよう。 公式 公式 4点が同一平面上にあるときは、公式2個 2 まとめ 以上が、空間ベクトルの公式一覧です。 平面ベクトルの公式は「 平面ベクトル 公式一覧 」で説明しているので、チェックしてみてください。 この単元の公式を、PDFファイルでプリント1枚

ベクトル １５ 空間ベクトルの大きさ計算 怜悧玲瓏 高校数学を天空から俯瞰する

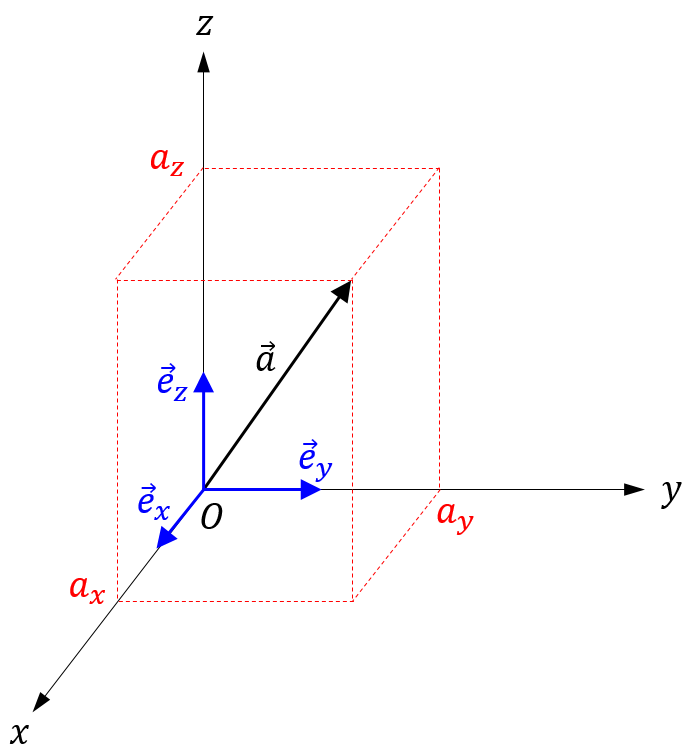
ベクトルの成分表示と座標変換 力学の道具箱 スカイ技術研究所ブログ

空間ベクトル → OP = (x y z) の大きさは，線分 OP の長さである．いま，この線分の長さを求めてみよう． 点 P から， xy 平面に下ろした垂線の足を H とすると， H の座標は (x, y, 0) であるから，三平方の定理より OH2 = x2 y2 である．また， POH は H を直角とする直角三角形であるから，再び三平方の定理より OP2 = OH2 PH2 = x2 y2 z2空間のベクトルの要点です。 空間における点の座標からベクトルの成分、内積、方程式や図形との関係をまとめます。 平面ベクトルで定義や定理はまとめてあるのでここでは成分を1つ増やした程度で済ませます。 空間の点 空間における13 ベクトルと空間の 3 次元ベクトルの内積の成分表示 図10 空間ベクトルの成分表示 z x x 1 z 1 0 y 1 y a＝ x 1 y 1 z 1 図10 で表されるa の成分表示は, a＝ となり, その大きさ (ノルム) は, xa 2＝√ 1 ＋y 1 2 ＋z 1 2 となる。 さらに, 3 次元ベクトルの内積 の成分表示は次の通りである。

平面幾何におけるベクトル演算 内積と外積

ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ

この映像授業では「高校 数学b 空間ベクトル11 面積公式」が約15分で学べます。問題を解くポイントは「面積公式のルートの中は、"（絶対解析学において、ノルム は、平面あるいは空間における幾何学的ベクトルの "長さ" の概念の一般化であり、ベクトル空間に対して「距離」を与えるための数学の道具である。ノルムの定義されたベクトル空間を線型ノルム空間または単にノルム空間という。 ものによっては絶対値や賦値（附値、付値）と呼ばれることもある。また、体の拡大におけるノルムや、多元 空間ベクトルの問題なので、成分が（x,y,z)の3つになりますが、 平面ベクトルの場合とする事は同じなので、すぐに慣れるはずです。 問題 xyz空間中に、点A(2,0,0)、点B (0,1,0)と ベクトルu\(\vec {u}=(1,2,5)、ベクトルv\vec {v}=(1,1,1)\)

数学b 空間ベクトル 3 1 空間ベクトルの内積 Youtube

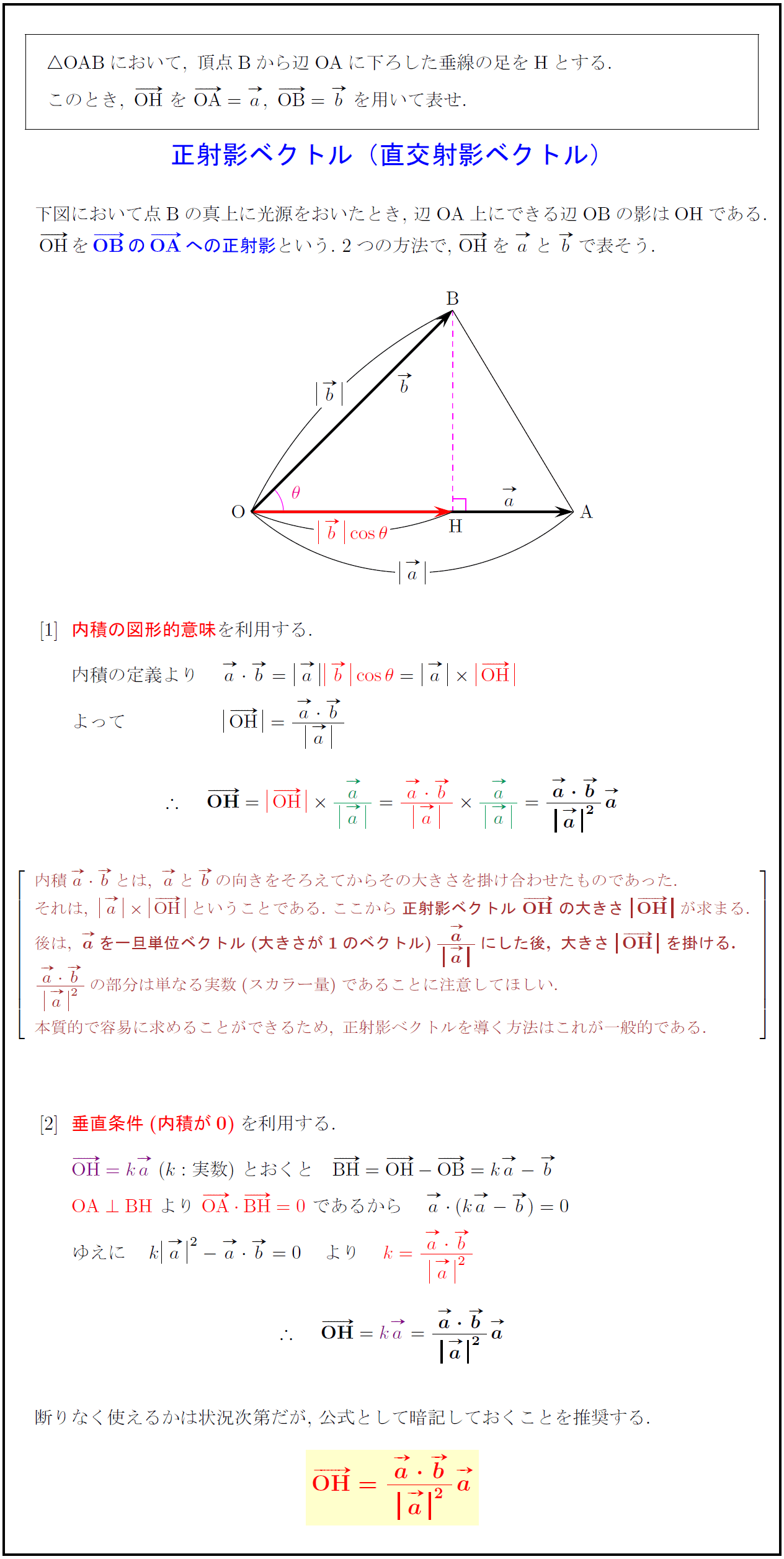
高校数学b 正射影ベクトル 直交射影ベクトル 受験の月

空間ベクトル（くうかんベクトル、ドイツ語 Vektor, 英語 vector, ラテン語 vector, 「運搬者、運ぶもの」より）は、大きさと向きを持った量である。ベクタ、ベクターともいう。漢字では有向量と表記される。ベクトルで表される量をベクトル量と呼ぶ。 例えば、速度や加速度、力はベクトルである。平面上や空間内の矢印（有向線分）として幾何学的にイメージされる24 ベクトルの内積と大きさ ベクトルa とb について、それらがなす角度を とするとき a b = jajjbjcos をベクトルの内積という。二つのベクトルの内積を取った結果は通常の数となる。特 に、互いに直交する（なす角が90 度である）ベクトルの内積はゼロである12 外積(ベクトル積) 空間ベクトル(3 次元ベクトル) a,b (‰ 0) が平行でないとき, a,b の両方と直交し, a,b,n が右手系(下で説明す る) となるような大きさ1 のベクトルn が一意に定まる このとき, a,b のなす角をθ (0 ő θ ő π) として, a とb の外積aˆb を

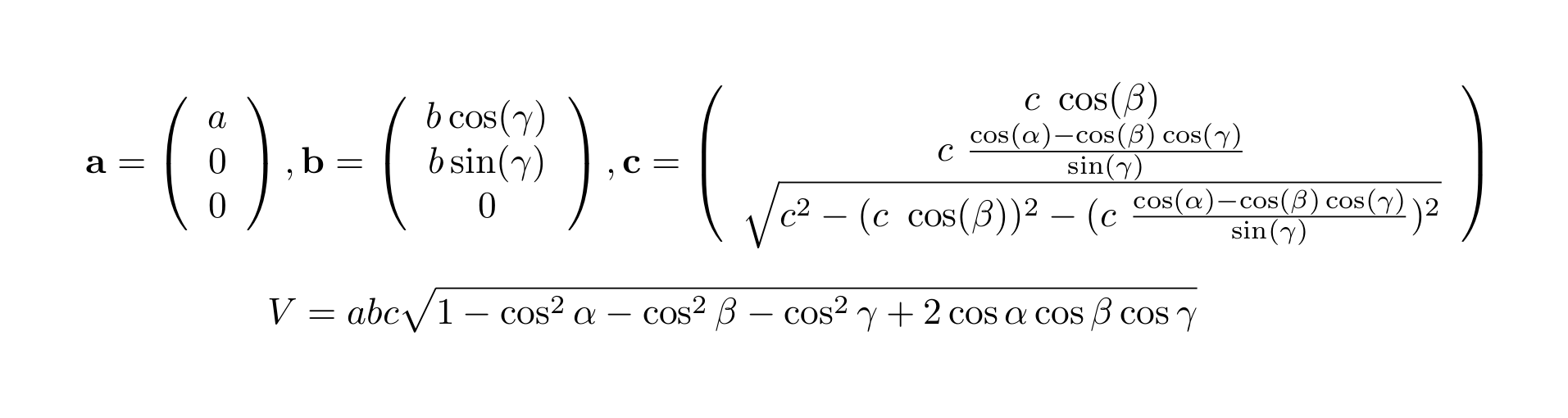
逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction

はじめて学ぶベクトル空間 大日本図書

空間におけるベクトル 次に3次元空間上におけるベクトルを考察する。 2次元空間上ではベクトルは2つの量の組み合わせで表わされた。 これは1つのベクトルはx軸方向に対応する量とy軸方向に対応する量の2つを持っている必要があったからである。 ベクトルの外積とは、空間において2つのベクトル a →, b → が与えられたときに、2ベクトルのなす角を θ とすると、両方のベクトルに垂直な大きさが a → b → sin ⁡ θ のベクトルのことを指します 。 ベクトルの内積はスカラー (単なる数値)だったのに対し、 外積はベクトルである ことに注意しましょう。 外積を求めるときの演算には×の記号を使います 空間ベクトルでは成分が1つ増えるだけです。 \(\vec{a}=(\,x\,,\,y\,,\,z\,)\) の大きさは \(\hspace{10pt}\large{\color{red}{\vec{a}=\sqrt{x^2y^2z^2}}}\) です。 これは 原点とベクトルの終点との2点間の距離に等しい ので忘れないようにしておきましょう。

ベクトルのなす角度 Thoth Children

ベクトルを総まとめ 意味や各種公式 重要記事一覧 受験辞典

空間の3つのベクトルa, b, cが同一平面上にないとき， kalbmc =0⇐⇒ k = l = m =0 空間内の任意のベクトル v は a, b, c の 1 次結合 v = ka lb mc で表され，5–1 2 次元ベクトルから3 次元ベクトルへ この節で学ぶこと 3 次元ベクトル，内積，空間座標 ★ 3 次元ベクトル 3 次元ベクトルの成分表示：a =(a x,a y,a z), b =(b x,b y,b z), ··内積：a·b = abcosθ ベクトルの大きさ：a = √ a·a 2 つのベクトルの間の角：cosθ = a·b abとなる。このときベクトル −→ a の大きさ fl fl−→ a fl flは 2点O、A間の距離OA (= 線分OA の長さ)であるから前ページより fl fl−→ a fl fl = fl fl fl −−→ OA fl fl fl =OA= q a 2 1 a 2 2 a 2 3 (ベクトルの大きさ) となる。 例1 A(1,2,3) , B(5,8,12)に対し、 −−→ AB = (5−1,8−2,12−3) = (4,6,9) だから fl fl fl −−→ AB fl fl fl = √

高校数学b 空間ベクトルのなす角の計算 映像授業のtry It トライイット

空間ベクトルの定義 数学b フリー教材開発コミュニティ Ftext

ベクトルの大きさを求めるときに2乗してから求めることもあります。 とすると なので、 シータ 新しい公式に見えるけどさっきと同じだよ 先ほど解説した公式では、ルートを使いましたがこの公式ではルートを後回しにできます。 空間ベクトルの成分と大きさ ↑答えが分かったら画像をクリック↑ 成分の計算 ↑答えが分かったら画像をクリック↑ 空間の2点を結ぶベクトル ↑答えが分かったら画像をクリック↑ 空間の分点 ↑答えが分かったら画像をクリック↑

高校数学b 空間ベクトルのなす角の計算 映像授業のtry It トライイット

行列の証明 わかる方回答お願いします Clear

48s96ub7b0z5f Net Kuukan Bekutoru Heimen

高校数学b ベクトル表示の三角形の面積公式 映像授業のtry It トライイット

ベクトル方程式をわかりやすく解説 直線 円の式から媒介変数まで

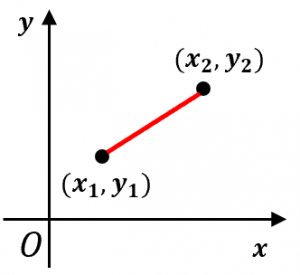
二点間の距離を求める公式 2次元 3次元 具体例で学ぶ数学

基礎の基礎編その１ 内積と外積の使い方

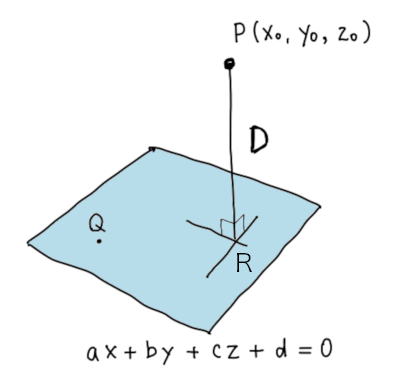
点と平面の距離 ベクトル解析 基礎からの数学入門

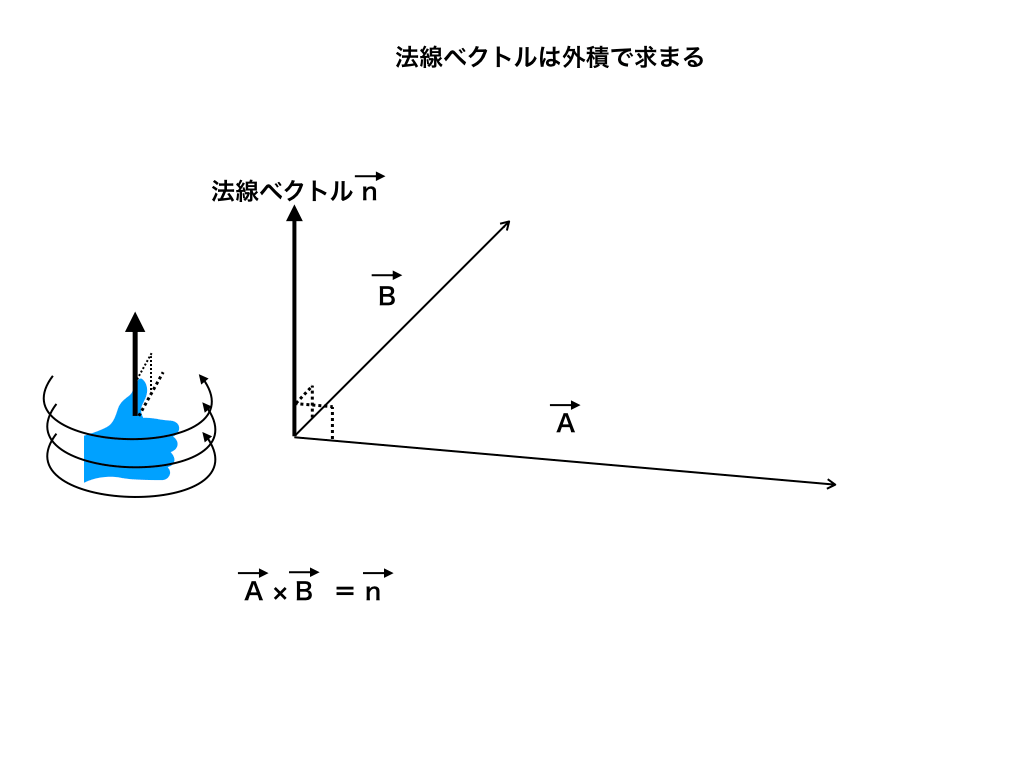
法線ベクトルの求め方と空間図形への応用

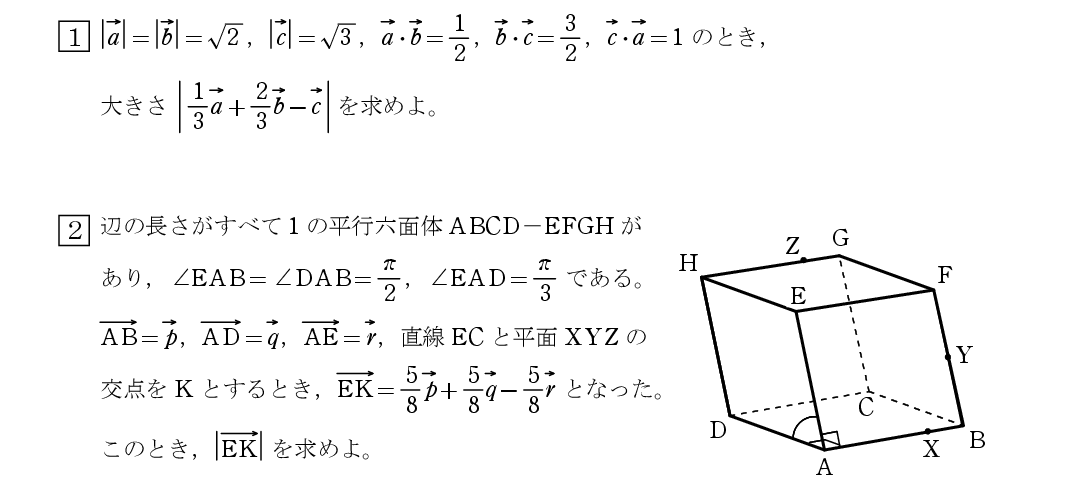
ベクトル １５ 空間ベクトルの大きさ計算 怜悧玲瓏 高校数学を天空から俯瞰する

ベクトルの大きさの最小値 ベクトルの大きさの最小値とその時のtの値 数学 教えて Goo

ベクトル編 高校のベクトルを基礎から復習 A 大学1年生もバッチリ分かる線形代数入門

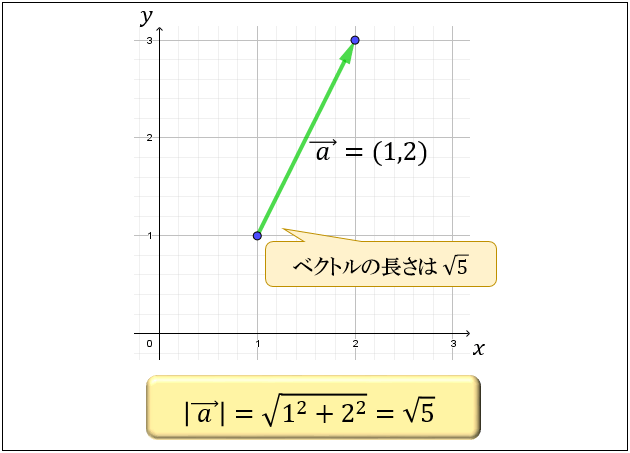
ベクトルとは何か その意味とベクトルの足し算 引き算 アタリマエ

ベクトルの大きさの計算方法 二次元 三次元

数学b編 完全攻略 高校数学の公式全部まとめてみたwww Cupuasu クプアス

1

ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示

ベクトル 高校物理の備忘録

空間ベクトルの内積 数学b フリー教材開発コミュニティ Ftext

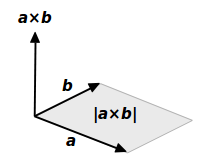
ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門

外積とは何か ベクトルの外積の定義 意味 大きさについて アタリマエ

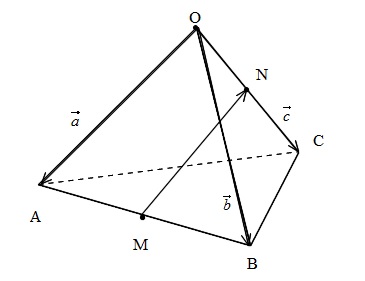
空間図形におけるベクトルの内積の使い方

Studydoctor空間上での三角形の面積 数ｂ Studydoctor

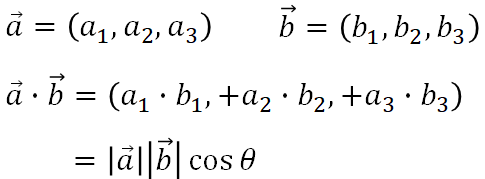
Python Fem 空間ベクトルの外積と内積 Snow Tree In June

1

数bのベクトルの問題です一辺の長さが２の立方体で 内積afベクトル Fcベク Yahoo 知恵袋

ベクトルとは何か ベクトルの意味と使い方

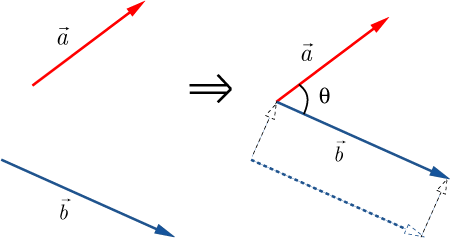
ベクトルのなす角

1

平面の方程式と点と平面の距離 おいしい数学

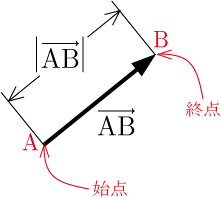
ベクトルの大きさ

Amazon Co Jp クリアファイル数学b空間ベクトル ダブルポケット サイズ おもちゃ

数b ベクトル 内積 垂直で大きさが４ Youtube

48s96ub7b0z5f Net Kuukan Bekutoru Naiseki

数学b 単位ベクトルの求め方とは 平行 垂直な場合の求め方も解説 数スタ

勉強しよう数学 3次元ベクトルの分解の公式

数学ｂ 空間ベクトルの基本と分解のやり方とコツ ページ 2 教科書より詳しい高校数学

外積を利用した2つのベクトルに垂直なベクトルの求め方とは 大学入試数学の考え方と解法

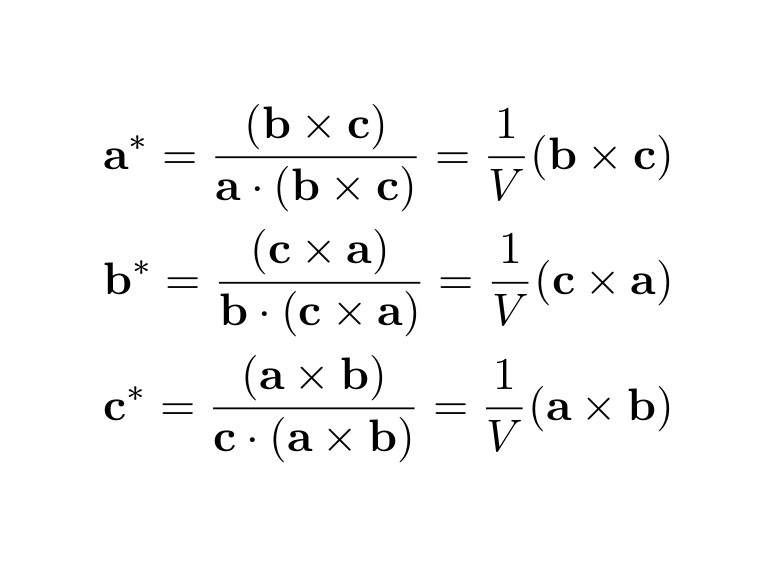
逆格子点の計算の理論背景 Theoretical Background For Calculation Of Reciprocal Lattice And Reciprocal Lattice Points To Cause Diffraction

第8回 基礎数学

48s96ub7b0z5f Net Kuukan Bekutoru Menseki

高校数学b 2つのベクトルに垂直な単位ベクトル 受験の月

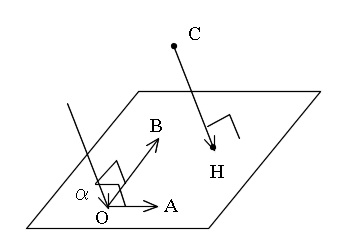
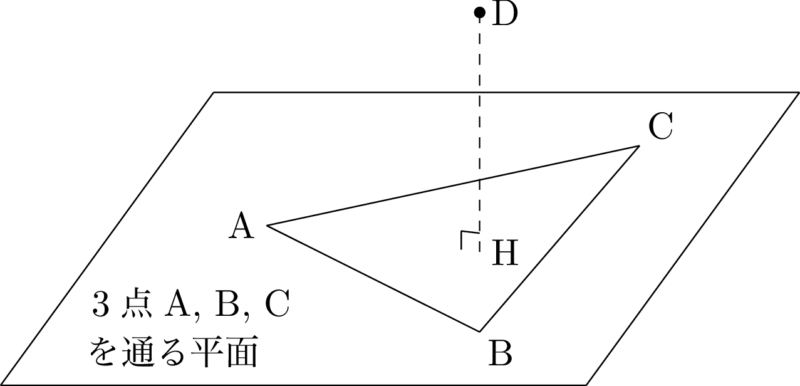
空間ベクトルで点から下ろした垂線と平面との交点を求める方法

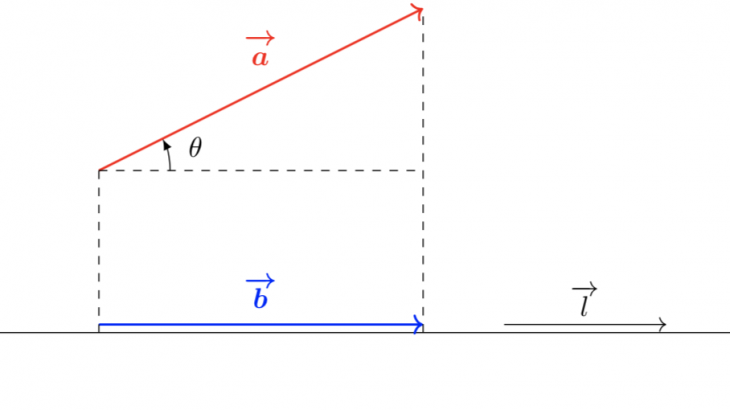
正射影ベクトルの公式は 平面や空間での入試問題を東大医学部生が解説 東大医学部生の相談室

ベクトルの大きさの求め方 なぜ2乗の公式で求められるの

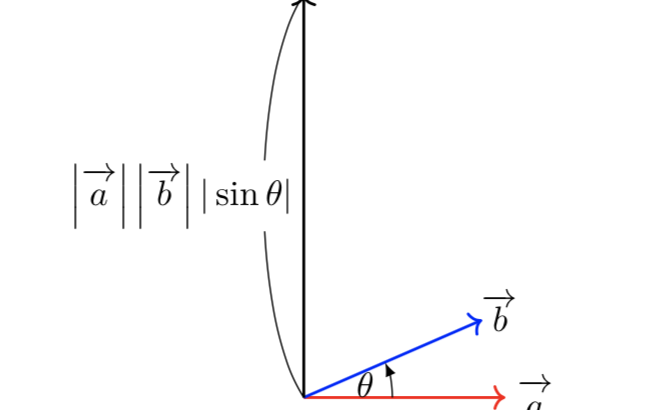
ベクトルの外積の公式やその覚え方とは 高校範囲で役立つ場面についても解説 東大医学部生の相談室

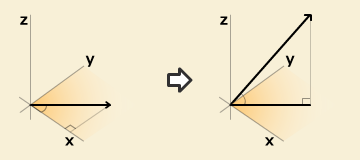
ベクトルの大きさ 長さ を求める計算式と計算ツール Peko Step

平面ベクトル 大きさの最小値 成分 Ver オンライン無料塾 ターンナップ Youtube

48s96ub7b0z5f Net Kuukan Bekutoru Seibun

勉強しよう数学 3次元ベクトルの分解の公式

中堅国立レベル 空間ベクトル長さの最小値 Cupuasu クプアス

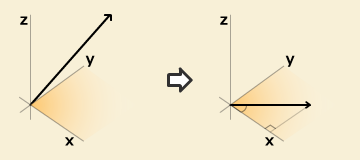
ベクトルの大きさ 長さ を求める計算式と計算ツール Peko Step

Studydoctor空間ベクトルの大きさと最小値 数ｂ Studydoctor

Studydoctor立方体と空間ベクトルの内積 数ｂ Studydoctor

第8回 基礎数学

数bの問題です 空間ベクトルの範囲です なぜ下線部のようになるかわかりません Clear

ベクトル １６ 空間ベクトルの内積計算 怜悧玲瓏 高校数学を天空から俯瞰する

高校数学b 平行六面体と空間ベクトルの演算 受験の月

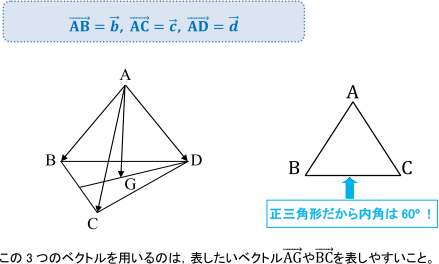
空間ベクトル 垂直であることの証明の仕方 数学b 定期テスト対策サイト

基本 ベクトルの成分と演算 なかけんの数学ノート

テストに出た 高校数学ｂ空間ベクトル２ 空間のベクトル 対策まとめ問題集 答え 解説授業動画付き ブログやる気先生の 逆転の数学

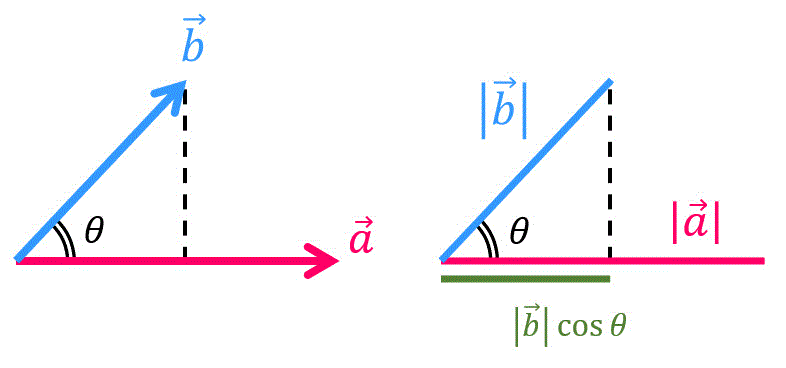
うさぎでもわかる線形代数 補充1 線形代数におけるベクトル 内積と外積 工業大学生ももやまのうさぎ塾

基本 立方体と空間ベクトルの内積 空間ベクトル3 01 Youtube

ベクトルを別のベクトルに射影したい Thoth Children

Studydoctor空間ベクトルの成分と演算 数ｂ Studydoctor

空間ベクトル ４ 大きさの速算 怜悧玲瓏 高校数学を天空から俯瞰する

平面ベクトル問題 京極一樹の数学塾

Math02 ベクトル Actionscript 3 0 For 3d

高校数学b 空間ベクトルのなす角の計算 例題編 映像授業のtry It トライイット

ベクトル 高校物理の備忘録

ベクトル １６ 空間ベクトルの内積計算 怜悧玲瓏 高校数学を天空から俯瞰する

東大落ちの慶應生による受験勉強法のブログです まだまだ書きかけです

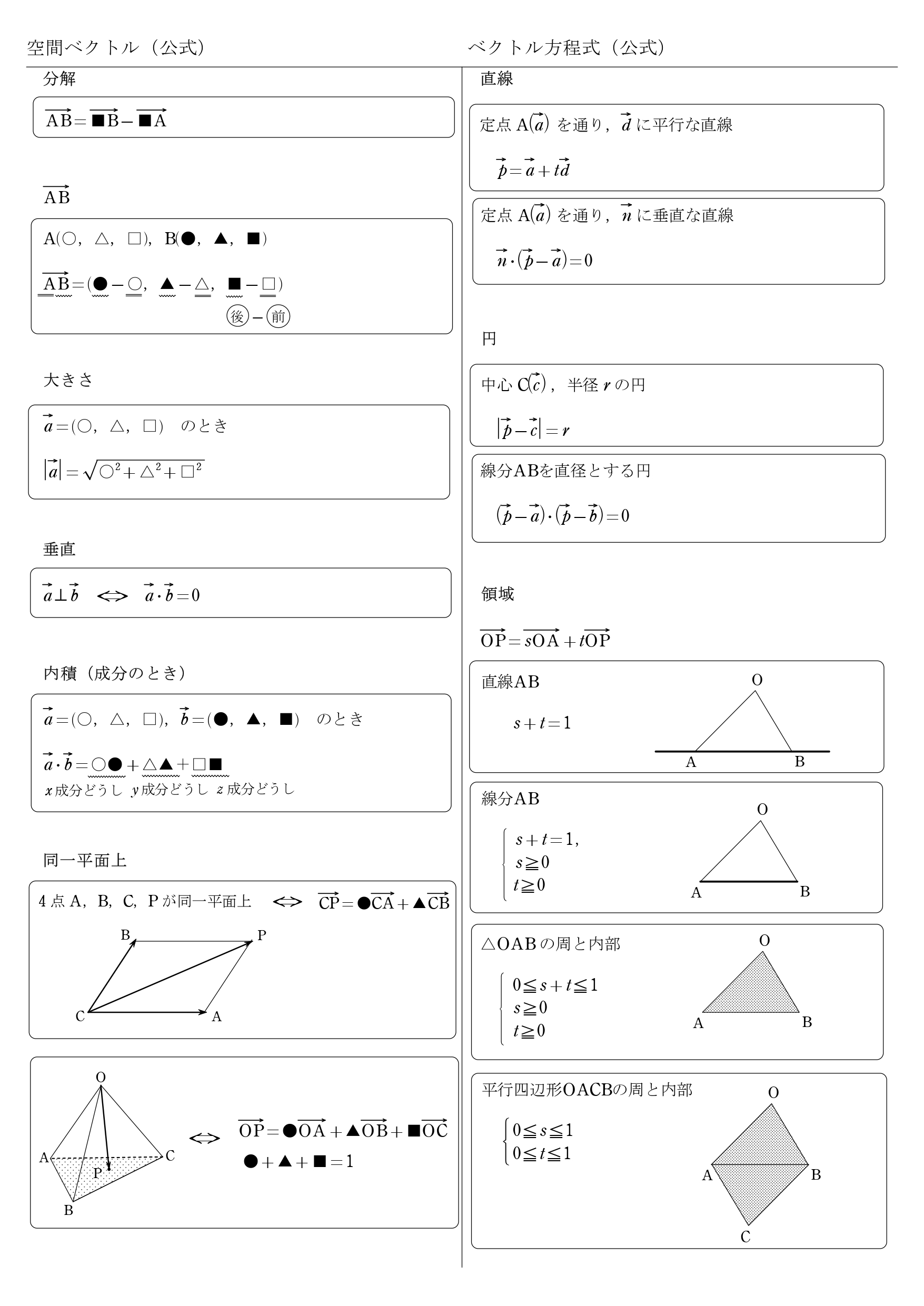
高校数学ｂ 空間ベクトル 公式一覧 ４点が同一平面上 学校よりわかりやすいサイト

空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典

Q Tbn And9gcqhlj8sap4tc500xqvdi 3wi2bkr2fisrk6iarcjxbkzo2uwjfp Usqp Cau

そもそも位置ベクトルって何 基礎から丁寧に解説します 高校生向け受験応援メディア 受験のミカタ

高校数学b 余弦定理のベクトル表示と内積の定義の成分表示の証明 受験の月

数学ｂ 空間ベクトルの成分と大きさの求め方とコツ 教科書より詳しい高校数学

空間ベクトルの問題ver マーク方式の数学の問題を作ってみた

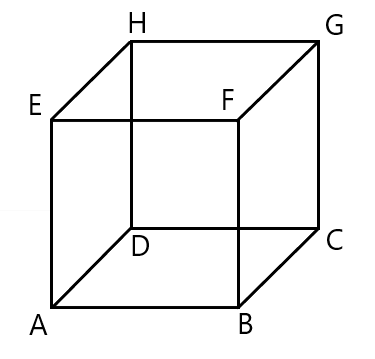
空間ベクトルの大きさ1 アドウィンテクノ塾

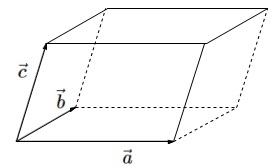
空間ベクトルの要点

空間ベクトル 外積 東大合格コム

高校数学b 空間ベクトルの垂直条件 練習編 映像授業のtry It トライイット

成分表示された空間ベクトルの大きさ 数学b フリー教材開発コミュニティ Ftext

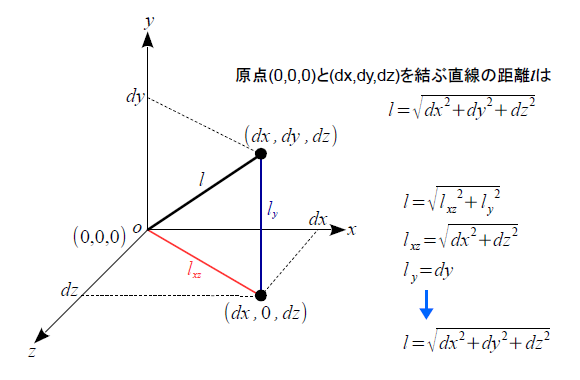
数学関数 ２点間の距離 ３次元 ゆるゆるプログラミング

ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ

Incoming Term: 空間ベクトル 大きさ 公式,